Jay Fisher - Fine Custom Knives
New to the website? Start Here
"Raptor"
A knife blade is a curious thing—it's expected to be made strong, wear resistant, and often corrosion resistant. It's also expected that a blade has some kind of stiffness, or flexibility, depending on the geometry, design, and intended use. When a knifemaker designs a knife, it's very important that he has understanding and proven long-term familiarity with the physical aspects of the steel blade, in order to make a useful, durable, and well-performing knife.
When I make a knife blade in high alloy steel, I cut out the blade, surface grind the blade to a pre-determined thickness, drill all the necessary holes, and, if it's a full-tang knife blade, I taper the tangs. I then accomplish the grinds (mostly hollow but some flat grinds on very thin blades) and profile the edges. I then filework, and/or engrave the blade if desired. It is then ready for my heat treat. You can see these various steps on my "Where's My Knife, Jay?" page and get an idea how this is done on my Shop and Studio Pages One and Two.
Before I heat treat my blade, I hold it my hand and press sideways on the blade point with my thumb. This I do because I want to feel the geometry of the thickness of the point. I know it sounds a bit non-scientific, but when you've made literally thousands of knife blades, in all different styles and patterns (500 of my patterns here with links to over 800 photos of my knives), you develop an intuitive feel for the knife blade geometry, and a sensitivity for feeling deflection and force that is not a measurable thing. It is more of an experiential technique, based on observation, and one of the reasons that a lot of clients have come to expect an extremely well-balanced knife from me. When I do this slight manipulative assessment, I can tell whether the blade point is going to be too thick, too thin, too wide, underground, overground, or the geometry of the point needs improving. I'll make any substantial adjustments then, expecting what the outcome will be after heat treatment.
After heat treatment, hardening and tempering, I instinctively do the same manual deflection practice. I call it a practice and not a test, since a test would suggest a readable scalable numerical result (more on actual testing below). When I do this, I can feel that the blade is substantially stiffer, more resistant to sideways deflection after hardening and tempering. To me, it is remarkably stiffer, and this would make sense, since a completely different crystalline structure and allotrope set is established by heat treating and processing of the steel.
So imagine my surprise as I read and hear, over and over, that the stiffness of steel is fixed, that it never changes, no matter its condition or hardness! According to this belief, I couldn't possibly feel any difference, since the only two things effecting the stiffness of the blade are the steel's element (alloy) content and the blade geometry! According to this persistent belief, no matter how a blade or any other piece of steel is heat treated, it always has the same flexibility.
This is simply untrue.
The lie: "All knife blades have the same flexibility, no matter how hard they are."
Using the word "lie" might sound too harsh, but this mistaken concept is so common that it's clearly shocking to see it repeated, over and again, by people who should know a lot more about steel. This is the real problem. Many knifemakers who claim to know what they are doing are clearly uneducated, inexperienced, and underdeveloped in their field, yet their mistaken opinions about the physics of steel properties are somehow held to be true, when they are clearly, provably false.
Knifemakers—particularly on discussion forums—continue to perpetuate this ridiculous myth. No doubt they've read it or heard it somewhere, and actually believe that a knife blade that is hardened and tempered to 60C Rockwell has the same flexibility as one that's been hardened and tempered to 55C Rockwell. They continue this error and mistaken concept, insisting to new and novice makers that they are correct when they are astoundingly, shockingly, embarrassingly wrong! Sadly, these new makers skulk away with mistaken beliefs, and this is disgraceful.
Knifemakers believing this myth have even argued with me over the phone, claiming they are right, merely because some forum moderator or anonymous metallurgist has told them the same lie. They insist, over and over again, that all steel has the same flexibility, no matter how it's hardened and tempered, and the only thing that changes the flexibility of a knife blade is the thickness and shape (cross sectional geometry) and steel type. There are guys even calling themselves machinists and perpetuating this false belief.
This stubborn concept is in flatly wrong and clearly untrue, and it's provable with simple testing. Yet the falsehood persists not only among knifemakers but also among some engineers, machinists, and metallurgists that don't have any real world experience with this physical characteristic.
What in the world is this all about?
By the time you finish reading this page, you'll understand how this concept is flawed, the origin of the confusion surrounding it, and understand how you can physically prove the truth to yourself if you are the experimental type.
The truth is, flexibility in steel can be changed, depending on how it is heat treated, hardened and tempered. Read on; if you have the slightest interest in this, you deserve to know the truth.
The steel knife blade is substantially stiffer, more resistant to sideways deflection after hardening and tempering.
The knife blade is stiffer at higher hardness, and more flexible at lower hardness.
The knifemaker should understand and control this physical feature of the blade.
Translated:
First of all I apologize for the language in which I write but I would like, if possible, that the idea I express should contain as much as possible of what I feel and think.
I have read attentively a clarification that makes on your page about your experiences, studies and no less valuable concepts of what your career has shown in what you do and your retractors. It is not my custom to messianize people but I consider an act of infinite justice the recognition not only of excellence but also of humility and desire to contribute to the teaching that you offer and promote.
Throughout history it has been shown that it is always easier to disqualify and destroy (whenever possible) than to learn through effort and perseverance and that, far from achieving it with you, produces the opposite effect and exposes the false and the mediocre. Honestly, I do not think about the badness of these people but about the incapacity and the consequent mediocrity.
For more than ten years I have followed your work and your progress with attention; I think I have mentioned sometime as I admire the family union that you have and the remarkable atmosphere that is breathed in your study-workshop. Although your creations of knives and blades in general are a technological and beautiful spectacle, there are other related activities that also deserve recognition and admiration such as leather, stone, casting, photography, creation, design and construction of machines and tools and the impeccability and usefulness of your website ... and many more logically.
I have thanked you before but I do not find it redundant to repeat my recognition of what you have achieved with great sacrifice and dedication in all these decades.
Receive my extensive greetings of course to your family ...
Lic. Juan Herbut G.

Most knifemakers who insist that elasticity in blades is independent of hardness believe this because someone told them it was so, or because they read the basic theory that the modulus of elasticity is fixed in isotropic, uniform, crystalline structures. They discount the dramatic changes of the crystalline structure of heat treated steels.
In order to understand this issue, I'll cover a few concepts about materials, so you can get a grounded and basic idea of how they interrelate.
Elasticity, stiffness, and the Modulus of Elasticity are important concepts to the designer, the engineer, and the machinist. It starts at the atomic level. Metals have metallic bonding, that is, the atoms that comprise the structure of the crystalline form of metals have very strong bonds between them, yet the electrons in the outer shells can move freely among themselves. This forms a sort of cloud or sea of electrons in the metal, and because the electrons can move, metals can conduct electricity as the electrons move around. The crystalline structure has a basic, fixed form, that—in pure metals—is highly regular.
It takes a certain, definable force to displace these atoms from each other, or to pull them away from each other or to push them closer to each other. You can force the knife blade to deflect by putting your thumb on the side of the tip and pushing. Since this is not changing the physical characteristics or molecular or atomic structure of the steel, it is attributed to stretching out the interatomic spacing on one side of the blade, while compressing the interatomic spacing on the other. The force is removed and the blade then returns to its neutral position. It's easy to visualize if you consider that a crystal metallic form is a block comprised of a bunch of springs, in a regular, spaced arrangement in all three dimensions. When you pull, push, bend, or stretch these crystals, the metallic bonds distort in a very regular way. They can be pulled, and then when the pressure is off, they return to their stable positions. I emphasize stable because all materials have forces imposed on them at all times, even if it's just gravity, air pressure, or minimal loads created by their own geometry.
Because the bonds are atomic, and because they are chemically fixed, it is assumed that they are always the same. This is where the Modulus of Elasticity comes in. What it defines is how metals spring, or how stiff they are. The word modulus means a "constant factor or ratio." So, if one takes the word at its core, it is a very fixed and rigid number or ratio. The modulus of elasticity is a ratio. The ratio is stress to strain, or stress divided by strain.
Stress is the Load per Unit Area, or the amount of force put on a certain area of the material, and it's measured (in our terms) in KSI (thousands of pounds per square inch) or MSI (millions of pounds per square inch. There are other measurement methods—MPa, or megapascals and GPa or gigapascals. The easy thing to remember is that stress is measured in PSI (pounds per square inch).
Strain is the amount of stretch under load per unit length. Strain is simply a change in length or dimension. Simple enough!
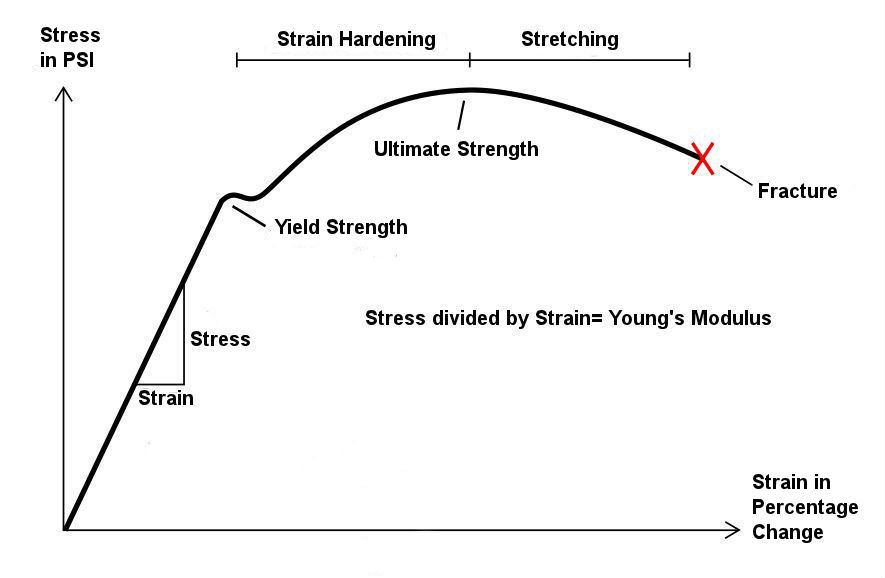
The Modulus of Elasticity comes from the linear portion of a stress-strain curve. It's also called "Young's Modulus of Elasticity" for the 18th-century English physician and physicist Thomas Young who developed the idea. This part of the curve is where the Modulus of Elasticity is derived. The modulus is the pressure (in PSI) divided by the strain (change in length) so is represented in PSI. Since the numbers are big, steel is typically represented in thousands of psi, or KSI. It's also represented in millions of psi, or MSI. In SI units, it's represented in pascals, or gigapascals. We'll stick with KSI since I am here in the United States.
The modulus of elasticity does not refer to the area of the stress-strain curve where the material is permanently bent (strain hardening, stretching) or breaks (fracture); it only refers to the linear (straight) part of the curve. In the graphic below, it's the straight, diagonal line where the strain-stress ratio (triangle) is shown.
Simple enough. For steel, the Modulus of Elasticity is a ratio, used to describe elasticity or stiffness of a particular material, measured in KSI or MSI, or thousands or millions of pounds per square inch.
Sometimes, scientists and metallurgists insist that what is changed in heat treating and processing in steel is a plastic property, and not the elastic property. They may claim that steel allotropic conversion of crystalline structure creating martensite, for instance, only affects the plastic property of steel while the elastic properties, being based on atomic arrangement, remain the same.
This is an error. The plastic properties of metal are clearly defined.
The two are completely different properties. Simply put, in elastic deformation, the metal springs back; in plastic deformation, the metal is bent or permanently deformed. In a knife blade, elastic deformation is okay, but plastic deformation is permanent and a ruined knife blade.
Another common error I've seen in discussions is confusing ductility with elasticity. In an effort to explain why there appears to be a difference in flexibility after heat treatment, some people claim that it's not a change in elasticity, but a change in ductility that accounts for the difference. This is wrong.
Ductility is a completely different property and in a very basic sense, it's the ability for a metal to be stretched into a wire or hammered into a thin sheet. I go into depth about ductility at this bookmark on my Blades page. Ductility is a plastic deformation property, so happens when steel is permanently deformed. Elasticity is simply the measure of movement when forced—strain when stressed—without permanent deformation. Elasticity is a definite, measurable property and it is not ductility, which is a plastic deformation property.
Please note that the modulus of elasticity in steels is highly temperature critical; the modulus changes dramatically at elevated temperatures. On this page, and in referring to knife blades, please note that all determination and discussion is at room temperature, since knife blades are used typically at this temperature.
You might think that elastic movement in steel is strictly measured, but this is rarely the case. In most cases, standard ratios are employed. These are long-established numbers referred to over and over again, in a generalized way in steels. In other words, the modulus of elasticity is seldom measured at all!
This is the first limitation. There are great devices for measuring this, so one wonders why so little actual measurement takes place. This is because not many engineers, metallurgists, or machinists are concerned with the elasticity of steels. They are usually much more concerned with the yield strength, ultimate strength, and fracture strength of steels. Since the actual elasticity is fairly uniform, it's not usually measured, but only established by formula, which, in most applications, is close enough. In industrial uses, and in engineering applications, the modulus of elasticity is not as important as yield strength. Consider that in a structure, a bit of flexibility is expected, but when the steel moves enough to permanently deform (bend) you have much more important issues! So, standardization and generalization of elasticity is accepted.
Below is a list of ways that the actual measurement of the modulus of elasticity is limited and thus, rarely used in high alloy steels. This applies specifically to knifemaking, where I know of no one who is actually measuring the elasticity of heat treated steels—except for me (see below)!
No knifemaker uses these tests, and rarely do machinists use them, since general standardized ratio is accepted. Simply put, knifemakers and knife manufacturers do not regularly test, plot, chart, and record the modulus of elasticity of various heat treated blades, and they simply accept a fixed number, which is 30 MSI.
Jay,
I wanted to thank you for your for your amazing website! I have spent countless hours reading and
rereading your pages and get lost in all the information you provide. I have learned so much from
your pages and knowledge in the knife making world. So I wanted to say thank you from a new knife
maker to THE master of knife making! Your knives are impeccable and your knowledge and techniques
unmatched! I strive to, one day, be able to make a knife half as good as the great Jay Fisher!
Thank you for everything you do for the knife making world!
Chad Filler

In a fixed, isotropic crystalline solid, the modulus of elasticity is independent of hardness.
When the crystalline allotropes are changed, so is the modulus of elasticity.
Transformation of steel by heat treating, hardening, and tempering changes the allotrope arrangement, volume, and ratios dramatically, thus changing the modulus of elasticity.
Because the modulus of elasticity is theoretically considered an inherent atomic property of metals, it is believed by some engineers, scientists, and metallurgists to be fixed. However, the crystalline allotropes of steel are not fixed. If you make a steel harder, by standard heat treating (hardening and tempering) it does not behave in the same manner as if left fully annealed. Also, a steel that is hardened and tempered to HRC 55 is dramatically different than a steel that is hardened and tempered to HRC 60. Any practical engineer or metallurgist realizes this, and so should every knifemaker.
Below, you will clearly see that scientists and researchers still argue this point, when it's easily demonstrable and proven. I'll reveal that below, also.
The mistake among knifemakers is more basic. Makers who have limited experience and low sensitivity to balance, force and stiffness requirements may only notice a dramatic difference in flexibility in thinner, smaller blades. They may not notice the difference between steel that is annealed and steel that has been hardened and tempered. They can't feel a difference, so they assume it must not exist. They read somewhere that Young's Modulus of Elasticity is fixed, so they defend the belief without ever actually testing it.
Simply put: most knifemakers who insist that elasticity in blades is independent of hardness believe this because someone told them it was so, or because they read the basic theory in beginning physics textbooks. The basic theory claims that the modulus of elasticity is fixed in isotropic, uniform, crystalline structures. They discount the dramatic changes of the crystalline structure of heat treated steels.
Another argument by undereducated knifemakers is that the only thing heat treating changes is the yield point. They go back and forth, confusing yield strength with elasticity, when the two are completely different. The truth is that both of these properties (the modulus of elasticity and the yield strength) change depending on treatment and the final temper of the steel. What also changes is the ultimate tensile strength, the corrosion resistance, the toughness, and a myriad of other properties, like the electrical conductivity and even the size of the steel! Heat treating and final temper changes everything! Yet, they want us to believe that the elasticity stays the same. No, it does not.
More crucially, another more disturbing revelation is that they are most likely failing in their heat treating process, and the allotropic changes are not dramatic or even noticeable. This is a much more serious concern, because it means that the overall treatment of the blade is incorrect, or at the least, suspect. There are a lot of badly heat treated steel knife blades out there, blades that are heat treated with torches or forges, blades that are quenched with snap temper, steels that are processed in large batches by heat treating companies and individuals that are more concerned with mass processing (and dollars) than with individually treated, premium processed blades. More about that on my Heat Treating and Cryogenic Processing of Knife Blade Steels page. If the maker heat treats his own blades and he does not notice a definite increase in stiffness after heat treating, he had better check his own process; it's not working correctly! More on colossal heat treating errors.
Below, I'll show you (and anyone who wishes to understand this) how to actually experience, see, and measure the dramatic differences in stiffness and elasticity of hardened and tempered steel depending on treatment.
"I believe it will change. Young's modulus has its origin in the nature of bonding including interatomic distances. In case of the heat treatment you have referred to that is quenching for hardening of steel it is martensitic transformation which leads to hardening. Martensitic transformation leads to trapping of carbon in the ferritic(martensitic) lattice and thus leads to larger interatomic separation as compared to diffusional transformation leading to formation of equilibrium ferrites. Therefore, there must be difference between Young's modulus of the steel in annealed condition (equilibrium ferrite) and hardened condition (martensite)."
"By how much? I have not seen a literature answering this. This difference is indeed of consequence when modeling mechanical behavior of a structure having annealed and hardened regions, like in case of weld joints. Unfortunately, this aspect has been neglected thus far and needs attention to improve accuracy of the computed results. In one of my experiments with the steel I work with I observed ~ 10% difference. However, it was a single experiment and I cannot publish this without having sufficient statistics. However, there is indeed a difference as suggested by the theoretical consideration as well as experimental observation, though the experimental observation needs to be reinforced with more experiments."
--Santosh Kumar, Bhabha Atomic Research Centre
Mr. Kumar makes a good point, in not seeing the literature answering this. Would it surprise him to know that the difference is much more than 10%?
Direct quotes from knifemakers that are unclear on the property of elasticity, and my summations in bold:
The truth is not so difficult to understand. If you have read my "Heat Treating and Cryogenic Processing of Knife Blade Steel" page, you'll realize that tremendous transformational changes occur not just in steels that have been heat treated, but also in steels that are finished at different hardnesses by changes in tempering.
One of the reasons I started making knives four decades ago was due to my interest in heat treating—that a piece of steel could be tremendously harder (or softer) than a piece of steel that was cut from the same bar. The difference in heat treating creates astounding changes, and these changes mostly occur while steel is in a solid state. Let's look at some simple manufacturing methods and data to get a deeper understanding of how elasticity, springiness, flexibility and the modulus changes depending on the material condition.
The professionals who manufacture springs have a real jump on the idea of elasticity. Sorry for the bad pun, but really, if you are one of the people who insists that a spring at 60 HRC has the same elasticity as a spring at 52 HRC, why would spring makers temper the springs back at all? Why not leave them at high hardness, since they will be less subject to wear? You might answer that high hardness means more stiff and brittle, and that the spring would break, and you would be correct!
Conversely, if the modulus of elasticity remains the same no matter the hardness, why not leave the springs fully annealed? That way they are not brittle, are very tough and unlikely to ever fracture. The truth is, annealed springs would lack elasticity! Springs are carefully hardened and tempered for a desired combination of elasticity, hardness, and toughness.
Springs are made in a variety of ways, and while most are hardened and tempered, some of them are work-hardened (strain-hardened). Work hardening is compressing and forcing the metal to have many interrupted dislocations. The more dislocations are pinned, tangled, and stopped, the stiffer the spring is! What? How can that be—when steel is supposed to have fixed elasticity independent of treatment?
It's common professional spring manufacturing practice to vary the hardness of springs by heat treatment, tempering, and strain-hardening to various degrees to attain the desirable "springiness" or elasticity of the steel. What is critically important is the crystalline arrangement and dislocations, which vary dramatically depending on the final temper!
Special note: if you actually believe that the elasticity of a spring is fixed no matter the condition of the steel, try this. Get a small coil (helical) compression spring and compress it with your fingertips. Feel it. Now, heat it up with a small butane or propane torch to dull red. Let it cool. Now, compress it again and you'll find that it looses all of its elasticity, and just bends like a piece of soft wire. Try the same thing with a coil (helical) extension spring. You'll find that after it's heated and cooled, you can just stretch it out permanently. What happened to the "fixed" elasticity?
It's simple. You've changed the crystalline structure and allotrope of the steel by heating it. You've actually annealed it, or tempered it to a softer condition. Because you have changed the fixed, isotropic crystalline solid, it has changed the modulus of elasticity.
Now here's one for consideration: an automobile has springs. They flex, they bear weight, and in time, they can weaken and sag. This is practical physics in action. If you don't believe that car and truck springs sag over time, then I suggest you enter the term "Automotive Springs Sagging" in any search engine to see how prevalent this is.
If the modulus of elasticity is fixed in steel no matter the condition of the steel, why do car springs sag over time? Why would they ever need replaced? Could it be that in time, the internal structure of the steel changes? Could it be that, by flexing or bearing load, changes are happening inside the steel? Of course there are changes, otherwise springs would last forever.
If changes happen in springs that effect their elasticity, so that bearing the same vehicle's weight actually makes them compress more, and more easily, then isn't there a variation in elasticity? Wait—I thought all elasticity was fixed in steel no matter the steel's condition, because the atoms are all still the same...
I'm only a practical knifemaker and machinist, but I can guess that crystalline changes within the structure of the steel might be responsible for the change in elasticity. Perhaps the change is caused by dislocations, perhaps because of work-hardening that embrittles tiny areas that then are subject to microfractures. Perhaps it is caused by changes in the temper of the spring as a result of the forces upon it. Perhaps it's caused by allotropic and solution changes in the steel's crystalline structure. No matter: the elasticity changes and it changes dramatically. Otherwise, springs would never sag, right?
Why would knifemakers say that elasticity is fixed in blades no matter the steel condition or allotrope set? Just like a spring, a knife blade can vary in its state, treatment, exposure, and use, and yet somehow a knife blade is more regular than a spring? Are knife blades somehow immune to the conditions that make car springs sag and weaken? Wait. maybe we should replace all automobile springs with knife blades just to be sure—plus it would look really cool!
Right there, the whole argument for fixed elasticity is erased. Just look at how springs are manufactured, conditioned, used, and aged and it will be clear that the combination of forming, heat treating, tempering, and working changes the spring to vary the elasticity. Elasticity of steels is not fixed and changes with hardness and condition of the steel.
Again, elasticity is fixed in a fixed, isotropic crystalline structure, but steel is NOT a fixed, isotropic structure. Steel is a varying allotrope with elements in solution.
If Young's modulus of elasticity does not vary in any particular steel type, why is it that on nearly every comprehensive data sheet about every modern steel, there is often a chart detailing a range of modulus of elasticity that varies depending on the heat treatment method? Why do knifemakers (particularly) ignore that variations in heat treatments produce substantially different elasticity in these steels, even when the manufacturer details this to the exact KSI or MPa? While it's sad that most "one-page" data sheets throw out the generalized 30MSI modulus, upon closer examination and inquiry, more detailed data exists, even though many steel foundries and suppliers do not include it in brief overviews like data sheets or white papers. By the way they also don't include treatment protocols for cryogenic processing, even though nearly all high alloy steels require a sub-zero or cryogenic temperature just to have complete martensitic conversion! The reasons this information is not included is detailed at this bookmark.
Knifemakers will discuss grain irregularities to the angstrom (they have no idea, no electron microscope, but do this on forums continually), all the while ignoring what the steel foundry has actually charted on their more detailed steel data documents. Good grief, if the steel maker can tell you how to vary the modulus, are knifemakers calling them liars claiming the modulus doesn't change?
A scalpel blade is a very small knife. The scalpel blade can be very hard and wear-resistant, but it will be less flexible. Here's a simple quote from a leading manufacturer of scalpels in Sheffield England, Swann-Morton:
"The hardness of the (scalpel)blade is determined by the heat treatment process and it involves striking a balance between hardness and flexibility. A marginally softer stainless blade tends to be more flexible however this can arguably lead to quicker edge deterioration during use."
A scalpel needs to have some controlled flexibility because insertion and removal from the handle requires flexing of the blade. It also needs to have wear-resistance, like any knife.
If this major medical scalpel company, employing about 1000 people with annual sales at over $53 million knows that flexibility of steel is associated with its hardness, why is this so hard for knifemakers to understand?
Here's a simple study, with a fairly common steel. This was presented in the Journal of Material Science and Engineering, published January 31, 2016, titled: "Analysis of Mechanical Behavior and Microstructural Characteristics Change of ASTM A-36 Steel Applying Various Heat Treatment" by Hasan MF, Department of Industrial Engineering and Management, Khulna University of Engineering and Technology in Bangladesh.
This is just one singular study; there are many like this, easily available for investigation on this vast knowledge base called the internet. It's interesting to note that this particular study is peer-reviewed and frequently referenced by hundreds of metallurgical scholars, so this is not some transitory document.
The study details treatment of a common structural steel. This is not a high alloy steel, it's A36, a mild carbon structural steel. It's important to note that high carbon alloys will demonstrate even a wider range of changes.
Note carefully the drastic, proven change in Young's Modulus depending on the condition and treatment of this common steel type in the column in red.
WHAT? I thought that the modulus never changes! And this is no small change! From the lowest value (annealed) to the highest value (hardened) is a variation of 304%! What? How is this even possible?
It's simple, really; it happens because of the differences in allotropes. From ferrite and cementite (pearlite) to austenite, to martensite, to ferrite/austenite/martensite/bainite combinations (with carbides): these are all drastic changes in the material, the crystalline structure, the arrangement, the density, the dislocations, and the overall properties. Even the final size of steel varies depending on the treatment, due to allotrope change!
Simply put, actual studies demonstrate a substantial change in the Young's Modulus and the elasticity of steel, depending on the heat treatment and condition! How could this be denied?
| Mechanical Properties of A36 Steel | ||||
| Heat Treatment | Tensile Strength MPa (KSI) |
Hardness (in BHN) |
Yield Strength MPa (KSI) |
Young's Modulus GPa (MSI) |
| Untreated | 402.45 (58.37) | 69.8 | 220.03 (31.91) | 207.88 (30.15) |
| Annealed | 389.34 (56.46) | 62.15 | 212.54 (30.83) | 302.32 (43.85) |
| Normalized | 452.13 (65.57) | 120.36 | 242.26 (35.14) | 288.12 (41.77) |
| Hardened | 734.32 (106.50) | 293.4 | 278.11 (40.34) | 632.47 (91.73) |
| Tempered | 421.76 (61.17) | 100.01 | 232.78 (33.76) | 293.63 (42.59) |
I don't know how much more clear this could be. Yet many knifemakers and even some engineers and metallurgists claim that Young's Modulus is fixed, independent of hardness and treatment. Wow.
The Young('s) modulus is generally weakly influenced by point and line defects. However, as mentioned by Santosh, it might change because of phase transformations. For instance, in the annealed state, the microstructure consists of alpha ferrite and cementite while the as-quenched microstructure may be fully martensitic. Because these different phases have different elastic properties, the young modulus may change during a heat treatment.
Serra Topal, Gazi University
The origin of this misplaced, incorrect, and persistent idea (that elasticity is fixed) is a bit obscure. There will be many arguments here; I'm sure I'll get plenty of hate mail for stating the simple fact that the springiness of steel changes depending on the heat treatment, hardness, and condition of the steel—even though it's easily proven.
To determine where this misunderstanding comes from is just conjecture, but I'll do my best to explain where I think it originates. If you disagree, please don't write me, because I'm not willing to carry on endless chatter about what is an easily provable physical property of steel that I've seen over and over again, on every knife I've made in the last 40 years. Write instead to the President, and insist that this physical property (variation in elasticity) is something you're sure doesn't exist, and force him to change all steel currently in use so that it will conform—
If you refer to most advanced physics textbooks, it quickly becomes clear that elasticity is not a simple property. In an effort for young minds to understand, beginning physics books at high school and introductory college level display crystalline atomic forms as a stack or square of balls on springs. They explain that these springs represent interatomic forces, and by stretching them or compressing them, you get elasticity. Since the springs (atomic bonds) don't change, the springiness doesn't either.
The reality of crystalline arrangement—particularly of steel—is much more complex. Stress-strain relationships of every crystal type are very different, and various arrangements become tremendously complicated. Pick up an advanced materials properties text, and you'll find yourself trying to solve six simultaneous equations and determinants, just for a single cubic crystal. But wait, the crystal is tetragonal and it's bent, and it's not aligned with other crystals in the steel. Then there are all these complex carbides interfering with force and strain location. And then there are the dislocations knotted up and pinned every which way...
This is not easy to grasp, so basic beginning physics concepts are chosen because they are simple to understand. These rudimentary models are repeated, and the simplest idea, though incorrect, seems good enough for most people.
Another idea is often repeated. Some knifemakers claim that if there is a change in elasticity, it's so small that it doesn't make any difference. I've seen this idea pop up recently, as more and more logical people question the false idea that elasticity in steels is fixed and independent of hardness. They claim that the tiny difference in elasticity isn't enough to notice.
They probably get this idea from the scope of structural engineering. Truly, if an I-beam with an 8" thickness is used to build a skyscraper, you won't notice a change in elasticity in a 20 foot length. However, structural steel is usually a high strength-low alloy steel, and not a piece of tool steel. A knife is not a structural member; it's a thin, narrow and lightweight piece of hardened steel. You will notice a 10%-15% change in flexibility, particularly if the blade is properly, thinly ground. Of course, most beginning knifemakers make big, thick, wide, blocky blades and they won't notice the difference no matter how their blades are treated!
The reality is proven by actual testing. Knifemakers seldom test their products, and this is a real shame. Test next!
"Technically, young's modulus depends upon the inter-atomic force vs. displacement profile. Heat treatment, which does not change the lattice structure, actually should not affect the modulus. If there is a transformation to martensite or other phases, yes it should change. But a simple heat treatment with no phase change should not affect the elastic constants.
--Hariharan Krishnaswamy, Assistant Professor at Indian Institute of Technology, Madras
Read carefully Dr. Krishnaswamy's quote above. It's clear that when heat treatment does not change the lattice structure, there is no change in the modulus. However, steel has dramatic and significant crystalline lattice structural changes (phase changes) not only in hardening and tempering but also at different final tempers! Because the lattices (and phases) are changed, the elastic modulus changes. Simple enough!
Here is a very simple, clear, and logical test that can be performed with a minimum of equipment and instruments. This test will absolutely prove that the elasticity of steel changes depending on the hardness.
If you don't believe it, please do not write me. Just follow the simple instructions below and do this test yourself, and you will be absolutely convinced of the facts. You won't be fooled by nonsense perpetuated on knife forums and discussion boards by hobbyists who are unfamiliar with proper heat treating of knife blades.
I did the elastic deformation test with O1 high alloy tool steel (photos below). I chose O1 because it's readily available, and is a good and common steel for knife blades and cutting tools. The same test could be accomplished with other steels. I did the test in conventional heat treatment method (with no cryogenics) because I wanted it to be simple, and others to be able to do it without cryogenic equipment. This is a standard, conventional heat treatment. I'm assuming that if you are a knifemaker, you have an accurate furnace, a hardness tester, and accurate measuring apparatus (calipers, electronic contact centering tool, height gauge and some standard weights help). Precision is important. So is repeatability. I repeated the test three times with three different samples at two hardnesses to eliminate any error. In other words, I used multiple gauges (pieces) and repeated the test 18 times to eliminate any slight variables or discrepancy. The results are remarkably consistent.
And that is the test!
Repeat it with all three rods at the two different hardnesses. Repeat it three times for each rod by taking the rod out of the vise, rotating it around its axis (not end to end) and placing it back in the vise. This assures that any variation in the grain structure of the rod will be eliminated (there was none in my test rods). This will assure consistency. Just make sure that you clamp the rod, get an unstressed height and then immediately measure with the weight (stressed). If your deflection (bending) varies more than two thousandths of an inch from previous measurements of the same rod and same deflection (with or without the weight), then repeat the test to improve your accuracy. You'll find that once you set it up, it's surprisingly consistent no matter how the rod is oriented about its axis in the vise. Using the logged measurements, calculate the difference in height of each rod with the weight and without.
Here is what you will find. The rods that are harder (at 60 HRC) deflect less than the rods that are softer (at 55 HRC). With the same weight, in the same location, they are stiffer and deflect less. How much less? My experiment proved that it was between 13-13.5% Yes, the test varied less than half a percent with six samples and 18 tests.
Thirteen percent is a lot. You might not think so, but it is substantial. And this is with conventionally treated O1, not annealed vs. hardened, not cryogenically treated, not multiple tempered: simply conventional treatment. As one engineer told me, "13 percent doesn't seem much, but cut off 13 percent of your body (any part) and see how that changes things."
Okay, that's a bit dramatic; we're not talking about pruning; we're talking about flexibility. So imagine this: if a 6" (15.24 cm) long blade of a fillet or boning knife flexes 1.5" (3.8 cm), the change in heat treatment can mean an increase in flexibility to 1.75" (4.45 cm) at the same force. This may not seem like a lot, but to the knife user it is substantial. It will dramatically change the feel and the flex of the blade. Imagine what will happen if the temper is knocked back to 53 HRC or 50 HRC.
If the aim is to reduce the flexibility and increase stiffness, know that a blade that flexes 1/16" inch at the tip at a lower hardness may be stiff enough at higher hardness to have undetectable movement at the same force. And that is stiffer indeed!
"From a physical point of view, the Young modulus of a metal is linked to the second derivative of the atomic potential energy curve, so by the stiffness of the atomic bonding. Each atom or couple of atoms have its own stiffness. Then if you add to a steel solid solution atoms (for instance W) with a higher stiffer bonds, you will increase the Young modulus of your steel.
In addition, the presence of different phases (with different Young modulus) will change the modulus of your material and in a first approximation you may evaluate this change by the rule of relative amounts. Higher content of a stiff (high modulus) phase you have, higher will be the modulus of the material.
With this two ideas, you may consider that when doing a thermal treatment you are changing the amounts of solid solution atoms (which will precipitate), as well as the amount of precipitated phases. Consequently, depending on the involved atoms and phases the final result of your material (steel or other) will undergo a change of the Young modulus.
There is another last factor that you have to consider. Dislocations contribute to an easy deformation of the material and so they can start moving at low stresses and giving you a lower slope on the stress-strain curve. Be careful because strictly this is not a change of the modulus value, but a softening of your sample which exhibit a very low micro-yield point. However dislocations can also contribute to a decrease of the intrinsic modulus because around the core of dislocations there is an increase of the interatomic distances, which have associated a decrease of the stiffness of the atomic bonding and consequently of the modulus of the material at local scale. So if you have a strongly deformed material (high density of dislocations), you may have a slight decrease of the modulus, in spite that you could have a hardening of the material (increase of the yield point) by work-hardening. Pay attention because there are two different concepts.
Nevertheless, in most of cases, a high hardness is obtained because of the precipitation of hard and stiff phases, as well as because of blockage of dislocations by strong point defects interaction (usually weight atoms) and in those cases you will have also an increase of the modulus. If the value of the Young modulus is a critical parameter for you computation by FEA, I recommend you to ask some colleague to measure the real modulus of the samples by a vibrating resonant equipment. The resonance frequency of the sample will give you a more reliable value of the modulus than the stress-strain curve. I hope that my answer could be useful for you."
Jose San Juan, Materials Science, Condensed Matter Physics, Materials Physics
Professor
Universidad del País Vasco / University of the Basque Country, Public university in Leioa, Spain
Dr. San Juan clearly explains the resultant change in elasticity or stiffness of steel at various hardness and tempers. Steel does change depending on the hardness and crystalline structure, and the only way to know how much is to measure it!
Simply claiming the stiffness and elasticity is fixed in heat treated steels is incorrect.
Where do you go to get a certification as a "Knife Metallurgist?" Is there some specialized degree and classification awarded to someone who specializes in knife metals? Just what the heck are knife metals anyway?
This is a totally made-up title. If someone tells you or states (on every single knife forum while begging for money) that they are a "Knife Metallurgist," just ask them how many knives they've made. Ask them what specific education or degree is bestowed upon "regular" metallurgists that qualifies them to be "Knife Metallurgists." There simply is no such thing.
There are many people who are associated with the knifemaking field, and what is very informative is to follow the money. Suppose a person is begging for website donations while gleaning charts, graphs, and data from high school physics textbooks and college level introductory level metallurgy books. All of the information "presented" is available from many free sources on the internet that are not asking for money.
What would be the reason for this? Is it to ingratiate himself into a knifemaking community without actually being a knifemaker, much less, a professional knifemaker? Is it to donate his time and effort into educating knifemakers who don't actually know anything about the steels they use? Or is it to get money, via donation, just like a traffic and referral site, but without any of the bothersome traffic and referral activity? This person is not just throwing out data and photos gleaned from the internet and asking for cash, is he?
Just so you know, using text, data, and postings from other websites without written permission to make money is a federal felony offense of copyright infringement. It is not against the law to use this information for critique, education, and demonstration, however you are not allowed to directly make money from others' material without their written permission. You see, it's the money thing that's wrong. Building your website on the works of others while asking for dough is not only slimy, it's a time bomb and the first time someone decides to sue there's going to be big trouble...simply put:
United States Copyright Law {Section 102, Section (a)5}. It is illegal to cut, copy, paste, and use the photographs of others for any representation, presentation, web site, reproductions, or copies. If you use it for profit, it is a Federal offense!
The clock is ticking on these donation sites. While some people have become rich, many others are now being perp-walked into court and jail.
I don't normally pay attention to these venues, unless my name comes up, and then it's because some very nice person alerts me to this. A so-called "Knife Metallurgist" had represented the very same junior high school concepts I detail on this page with the springs and balls and such, and even referenced a "demonstration" that he thinks will certainly prove that elasticity does not vary with changes in hardness of the steel.
His demonstration was an utter failure and joke, because he referred as his "proof" to a YouTube video that displayed a poor, crude, ineffective, and wholly lousy novice technique! This is so, so bad... it's a video that demonstrates how to avoid any scientific method, and how to try to make a point with anecdotal, weak nonsense while looking like a hick. A third grader could have done a much better job.
The guy making the YouTube video used cast iron antique scale weights and two pieces of unknown, unidentified, different steels for a comparison! He's got a stainless steel ruler (unknown alloy, condition, or hardness) and a similar-sized piece of sheet metal (unknown alloy, condition, or hardness). He doesn't even know if they are the same size and thickness; they are two completely different pieces of steel that are just a bit similar in shape when you look at them with one eye closed... from a distance. This clown clamps them to a bench and drops his vintage weights (kind of) on the ends of the steel strips (no location specified, no accuracy required), and they both bend.
He says, "See? They bend about the same; I can't tell a difference."
Wow! Gravity confirmed! What a rock-solid scientific foundation on which to prove your point! Using this same scientific principle, I can't tell the difference between baking soda, heroin, or ricin, because they look the same!. Amateur hour... sigh. And the "Knife Metallurgist" uses this as his reference—that should tell you a lot! I suppose it was all the content he could find (for free) to justify his asking for your donation.
Both of these geniuses would be surprised to see the measurable difference in the test on this very page, but they would have to learn to use a caliper or a micrometer, and a dial indicator and try for accuracy. Clearly, the guy doing the YouTube video was no machinist, and any elementary school-aged child would have trounced him in the first round of the local science fair. What actual metallurgist would hitch his boat to this drivel? Please read the comments of actual metallurgists on this very page for some perspective—
Technically, any experienced scientific mind would know that when you are talking about 30 million PSI as a modulus, all measurements would have to be very precise and accurate, with minor deviations having substantial processed results. You're not going to get a thick piece of steel to bend with any measurable deviation by hardness unless you have massive weight. If you do, you'll need extremely accurate instruments to measure this, not a guy holding his thumb up to his eye with the tip of his tongue out for balance. This is why small, accurate pieces are measured in this type of demonstration, with instruments capable of measuring in thousands of an inch or less. In the metallurgical study referenced above, they used an ultrasonic resonance frequency detector.
On the site run by the so-called knife metallurgist, he makes the same claim as others, that the modulus of elasticity does not change in fixed, isotropic solids. This is true and correct.
However, steel is not a fixed, isotropic solid, it's a varying, allotropic solution. A real "Knife Metallurgist" would know that, wouldn't they? A real "Knife Metallurgist" would have experienced the difference in a soft, low hardness blade and a stiff, high hardness blade. This would happen when he had made dozens or hundreds of knives... right?
Someone posting on his site asked about this very page you are reading here at www.jayfisher.com.
The "Knife Metallurgist" said "Not all information on the internet is accurate. Even from experienced knifemakers."
Wow—did that weenie just call me a liar? And everyone who is referenced on this very page, real PH.D. metallurgists, research scientists, and professors? Did he call them liars, too?
This from a guy who's never made any knife? This from a guy who has never looked at any scholarly study of the matter (also directly posted on this page)? Where's the weenie's paper on the matter?
I'll offer that not all information on the internet is accurate, including from so-called made-up "knife metallurgists" who have no verifiable experience in actually making knives, who are running donation websites from common textbook data gleaned from other internet sources while claiming to be an expert.
If someone was truly a credible scholar, he would jump at the chance to disprove what he reads with his own accurate testing and demonstration. He would challenge the spring industry who—obviously—don't know what they are doing. He would challenge the peer-reviewed studies that contradict his position with his own research, experiments, procedures and theories on paper. This is what scholars do. They open themselves up to peer review through their documented studies. Instead, guys like this post charts and graphs taken from introductory physics books that—again and again—refer to the modulus of elasticity being unchangeable in materials that ARE FIXED, ISOTROPIC SOLIDS!
And then he refers to a goof-clown YouTube video as his source of proof!
Sorry for shouting, but here is the error, in my humble opinion as a knifemaker with 40 years under my belt: steels are not fixed; the allotropes are varied with dramatically different properties. You can experience these with proper heat treating which yields widely varying allotrope sets and solution microstructure variations. Of course, that would appear obvious if you are good at actual heat treating and cryogenic processing. You would think a knife metallurgist would know this, but evidently not.
You won't find "knife metallurgist," on any job description, on any course objective, on no degree, and in no place but on anonymous knife forums... go figure. And buddy, can you spare a dime?

If you have read this far, you might realize what is presented on most forums and discussion boards by well-meaning people may not be correct. There are some of them who, upon reading this will realize that they have been in error in claiming that the steel property of elasticity does not change depending on hardness or condition. There are some who will stubbornly disagree, and fiercely defend what they believe to be true. I've seen this all my career, and some people just refuse to learn or change.
[Special Note: about six months after I wrote this page, I noticed a distinct suppression on some of the knife forums about the claim of elasticity independence of hardness. It got curiously quiet when someone would bring up the subject. This is how I know that this very website is a worthwhile source of reference. Now, when a novice brings up the "springiness issue," there are few responsive comments, and some of those who once claimed there was no change to elasticity at varying hardness simply murmur, "just not much of a change." Uh-huh.]
If you question what you read here, I encourage you to begin testing yourself. It's very simple, logical and completely within the skill set of most knifemakers. Before you accept a premise, from me or anyone else, please consider their logic, their education, and their experience, and then try it out for yourself!
It's fun, it's clear, and your results will add to the understanding of steel properties in knife blades and we always appreciate more actual data!
At the very beginning of this page, I presented two scenarios and now I'll present the solutions.
Both of these scenarios I've had presented in my career, that's why I've cited them here.
Thanks for reading, and thanks for helping stop misconceptions, falsehoods, and wives' tales in our profession. My apologies to wives, everywhere!

| Main | Purchase | Tactical | Specific Types | Technical | More |
| Home Page | Where's My Knife, Jay? | Current Tactical Knives for Sale | The Awe of the Blade | Knife Patterns | My Photography |
| Website Overview | Current Knives for Sale | Tactical, Combat Knife Portal | Museum Pieces | Knife Pattern Alphabetic List | Photographic Services |
| My Mission | Current Tactical Knives for Sale | All Tactical, Combat Knives | Investment, Collector's Knives | Copyright and Knives | Photographic Images |
| The Finest Knives and You | Current Chef's Knives for Sale | Counterterrorism Knives | Daggers | Knife Anatomy | |
| Featured Knives: Page One | Pre-Order Knives in Progress | Professional, Military Commemoratives | Swords | Custom Knives | |
| Featured Knives: Page Two | USAF Pararescue Knives | Folding Knives | Modern Knifemaking Technology | My Writing | |
| Featured Knives: Page Three | My Knife Prices | USAF Pararescue "PJ- Light" | Chef's Knives | Factory vs. Handmade Knives | First Novel |
| Featured Knives: Older/Early | How To Order | 27th Air Force Special Operations | Food Safety, Kitchen, Chef's Knives | Six Distinctions of Fine Knives | Second Novel |
| Email Jay Fisher | Purchase Finished Knives | Khukris: Combat, Survival, Art | Hunting Knives | Knife Styles | Knife Book |
| Contact, Locate Jay Fisher | Order Custom Knives | Serrations | Working Knives | Jay's Internet Stats | |
| FAQs | Knife Sales Policy | Grip Styles, Hand Sizing | Khukris | The 3000th Term | Videos |
| Current, Recent Works, Events | Bank Transfers | Concealed Carry and Knives | Skeletonized Knives | Best Knife Information and Learning About Knives | |
| Client's News and Info | Custom Knife Design Fee | Military Knife Care | Serrations | Cities of the Knife | Links |
| Who Is Jay Fisher? | Delivery Times | The Best Combat Locking Sheath | Knife Sheaths | Knife Maker's Marks | |
| Testimonials, Letters and Emails | My Shipping Method | Knife Stands and Cases | How to Care for Custom Knives | Site Table of Contents | |
| Top 22 Reasons to Buy | Business of Knifemaking | Tactical Knife Sheath Accessories | Handles, Bolsters, Guards | Knife Making Instruction | |
| My Knifemaking History | Professional Knife Consultant | Loops, Plates, Straps | Knife Handles: Gemstone | Larger Monitors and Knife Photos | |
| What I Do And Don't Do | Belt Loop Extenders-UBLX, EXBLX | Gemstone Alphabetic List | New Materials | ||
| CD ROM Archive | Independent Lamp Accessory-LIMA | Knife Handles: Woods | Knife Shop/Studio, Page 1 | ||
| Publications, Publicity | Universal Main Lamp Holder-HULA | Knife Handles: Horn, Bone, Ivory | Knife Shop/Studio, Page 2 | ||
| My Curriculum Vitae | Sternum Harness | Knife Handles: Manmade Materials | |||
| Funny Letters and Emails, Pg. 1 | Blades and Steels | Sharpeners, Lanyards | Knife Embellishment | ||
| Funny Letters and Emails, Pg. 2 | Blades | Bags, Cases, Duffles, Gear | |||
| Funny Letters and Emails, Pg. 3 | Knife Blade Testing | Modular Sheath Systems | |||
| Funny Letters and Emails, Pg. 4 | 440C: A Love/Hate Affair | PSD Principle Security Detail Sheaths | |||
| Funny Letters and Emails, Pg. 5 | ATS-34: Chrome/Moly Tough | ||||
| Funny Letters and Emails, Pg. 6 | D2: Wear Resistance King | ||||
| Funny Letters and Emails, Pg. 7 | O1: Oil Hardened Blued Beauty | ||||
| The Curious Case of the "Sandia" |
Elasticity, Stiffness, Stress, and Strain in Knife Blades |
||||
| The Sword, the Veil, the Legend |
Heat Treating and Cryogenic Processing of Knife Blade Steels |